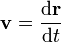Más precisamente, son las únicas partes I de R que verifican la siguiente propiedad:
si x e y pertenecen a I, x ≤ y, entonces para todo z tal que x ≤ z ≤ y, z pertenece a I.
Notación
Es un conjunto de números que se corresponden con los puntos de una recta o segmento, en el que se encuentra un
ordenamiento interno entre ellos. Los intervalos es el espacio que se da de un punto a otro en el cual se toman en
cuenta todos los puntos intermedios. Por ejemplo: en una recta tenemos un intervalo:[-2,2]entre este espacio se
encuentran los números (-2-1,0,1,2) aquí se encuentra un intervalo.....ya que el espacio abarca una serie de
números consecutivos que se corresponden entre sí.
También existe una regla ERRONEA para el uso del paréntesis: si se dibuja sobre la recta real dos intervalos adyacentes,
como (0; 1) y (1; 2) (es decir, se pinta la recta real y se coloca cuatro paréntesis donde corresponda), entre los dos
intervalos cabe un signo 1 (o lo que corresponda según los intervalos) cabe, apretado pero cabe. Mientras que si los
dos intervalos son (0, 1] y [1, 2), o (0, 1] y [1, 2) el número no cabe, o cabe muy estrangulado. O sea, que si los do
s intervalos son abiertos, el número 1 no pertenece a ninguno, y por tanto hay espacio para meterlo en medio.
admes potengamos en cuenta todo
|----------------|
Clasificación
Se pueden clasificar los intervalos según sus características topológicas (intervalos abiertos, cerrados y semi abiertos) o según sus características métricas (su longitud: nula, finita no nula, o infinita). Aquí están todos los casos posibles, con a ≤ b, y x perteneciente al intervalo, y l su longitud:
| Notación | Intervalo | Longitud (l) | Descripción |
|---|
![[a, b] \,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) | 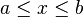 | 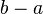 | Intervalo cerrado de longitud finita. |
 | 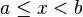 | 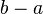 | Intervalo cerrado en a, abierto en b (semicerrado, semiabierto). |
![]a, b] \ \ \mathrm{ \acute o } \ \ (a, b] \!](http://upload.wikimedia.org/math/0/1/8/0189f84b7a0ea78dbc527c545d8c9598.png) |  | 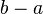 | intervalo abierto en a, cerrado en b. |
![]a, b[ \ \ \mathrm{ \acute o } \ \ (a, b) \!](http://upload.wikimedia.org/math/1/0/d/10d97baef8714cd0982a87681cfe4d1f.png) | 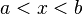 | 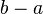 | intervalo abierto. |
![]-\infty, b[ \ \ \mathrm{ \acute o } \ \ (- \infty, b) \!](http://upload.wikimedia.org/math/0/9/7/097e7c70e6cbf2559d82fcb85f853033.png) | 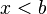 |  | Intervalo (semi) abierto. |
![]-\infty, b] \ \ \mathrm{ \acute o } \ \ (- \infty, b] \!](http://upload.wikimedia.org/math/e/8/2/e82cc38f6052cb558df6d0be418c5659.png) | 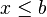 |  | Intervalo (semi) cerrado. |
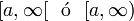 | 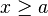 |  | Intervalo (semi) cerrado. |
![]a, \infty [ \ \ \mathrm{ \acute o } \ \ (a, \infty ) \!](http://upload.wikimedia.org/math/7/6/7/767d79359e390fb402d696537c7d6b24.png) |  |  | Intervalo (semi) abierto. |
![]\infty, + \infty [ \ \ \mathrm{ \acute o } \ \ (\infty, + \infty ) \!](http://upload.wikimedia.org/math/6/b/a/6ba8dc9071eaad7acf515f333bba45cf.png) | 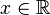 |  | Intervalo a la vez abierto y cerrado. |
 |  | 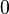 | intervalo cerrado de longitud nula. Es un conjunto unitario. |
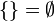 | x no existe | Sin longitud | conjunto vacío. |
Un intervalo abierto o cerrado (pero no semiabierto) de longitud finita se puede también definir
a partir de su centro y de su radio:
Si I = ]a, b[, su centro es c = (a + b)/2, y su radio es r = (b - a)/2. a < x < b
equivale a |x - c| < r; y se interpreta como la distancia entre x y c es menor que r; se nota x ε B (c, r); B para bola abierta, término que se generaliza a cualquier espacio métrico. De la misma manera, I = [a, b] corresponde a la condición |x - c| ≤ r. En tal caso se habla de bola cerrada.
Se nota este conjunto:
_
B (c, r) = { x ε R, |x - c| ≤ r }. Es la clausura topológica de la bola abierta B (c, r) = { x ε R, |x - c| < r }.
Cuando dos variables - pongamos x e y - toman sus valores en sendos intervalos I e J,
es legítimo preguntarse en que intervalo varían su suma, su diferencia, su producto y su cociente.
Contestar a esta pregunta permitirá definir las cuatro operaciones sobre los intervalos.
Tomemos I = [a, b] y J = [c, d]. Entonces a ≤ x ≤ b, y c ≤ y ≤ d.
podemos sumar las inegualdades: a + c ≤ x + y ≤ b + d. Lo que justifica que I + J = [ a + c , b + d ].
Para la diferencia, hay que mirar primero - y : - d ≤ - y ≤ - c, y luego se puede sumar las inegualdades:
a - d ≤ x - y ≤ b - c. De ahí obtenemos I - J = [ a - d, b - c ].
Si se toman a, b, c y d positivos no nulos, el producto y el cociente son también sencillos:
I · J = [ ac, bd ] y I / J = [ a/d, b/c ].
Generalización
Un entorno de centro a y radio δ es un conjunto de puntos cuya distancia a a es menor de δ. O sea: 
En particular si 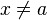 se denomina entorno reducido (E`).
se denomina entorno reducido (E`).  el cual no es un intervalo pues
el cual no es un intervalo pues- es un conjunto disconexo entonces se cambia la x por y o p












![[a, b] \,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png)
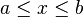
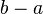

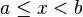
![]a, b] \ \ \mathrm{ \acute o } \ \ (a, b] \!](http://upload.wikimedia.org/math/0/1/8/0189f84b7a0ea78dbc527c545d8c9598.png)

![]a, b[ \ \ \mathrm{ \acute o } \ \ (a, b) \!](http://upload.wikimedia.org/math/1/0/d/10d97baef8714cd0982a87681cfe4d1f.png)
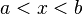
![]-\infty, b[ \ \ \mathrm{ \acute o } \ \ (- \infty, b) \!](http://upload.wikimedia.org/math/0/9/7/097e7c70e6cbf2559d82fcb85f853033.png)
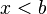

![]-\infty, b] \ \ \mathrm{ \acute o } \ \ (- \infty, b] \!](http://upload.wikimedia.org/math/e/8/2/e82cc38f6052cb558df6d0be418c5659.png)
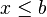
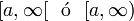
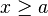
![]a, \infty [ \ \ \mathrm{ \acute o } \ \ (a, \infty ) \!](http://upload.wikimedia.org/math/7/6/7/767d79359e390fb402d696537c7d6b24.png)

![]\infty, + \infty [ \ \ \mathrm{ \acute o } \ \ (\infty, + \infty ) \!](http://upload.wikimedia.org/math/6/b/a/6ba8dc9071eaad7acf515f333bba45cf.png)
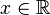


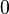
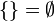

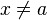 se denomina entorno reducido (E`).
se denomina entorno reducido (E`). el cual no es un intervalo pues
el cual no es un intervalo pues
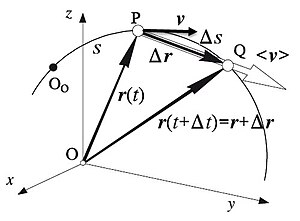
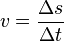 Definición de celeridad media:
Definición de celeridad media: